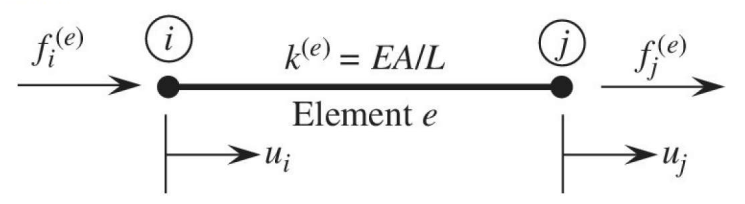Basics

When solving for the various items of interest using the finite element method (FEM) such as displacement, stress, and strain, it is important to understand the basics of what is happening when you start pressing the various mesh, boundary condition, and solve buttons. In software, these perform very complicated versions of the basics tasks outlined below.

At the most basic level, the FEM discretizes something into a set of nodes which form elements. The simplest form is a bar element, which represents a 1 dimensional spring with a node at either end and an element between the nodes with stiffness k. This stiffness can be a spring constant k, or if the model represents a real object such as a square bar , k can be calculated from the objects material properties and geometry.

Fig 1. Example bar element

With this model, we can develop a relationship between the forces f and displacements u of the nodes, connected by the element from Hooke's law, which relates spring force to displacement by the spring constant k.

	$f_i=k(u_i-u_j)$	(1)
	$f_j=k(-u_i+u_j)$	(2)

These can then be put into a matrix form by pulling out the common k terms and multiplying the displacement terms by an equivalent matrix. Review a numerical methods or linear algebra textbook for a deeper explanation of how matrix math works. This is the common way to represent finite element problems.

\begin{bmatrix}1 -1 // -1 1\end{bmatrix}

(3)